연결 리스트

3. 종류

연결 리스트는 그 구조에 따라 여러 종류로 나뉜다.

• '''단일 연결 리스트(Singly-linked list)''': 가장 단순한 형태의 연결 리스트로, 각 노드는 하나의 링크를 가진다. 이 링크는 다음 노드를 가리키며, 마지막 노드의 링크는 Null 값을 가지거나 빈 리스트를 가리킨다.

• '''이중 연결 리스트(Doubly-linked list)''': 각 노드가 두 개의 링크를 가지는 연결 리스트이다. 하나는 다음 노드(전방 링크)를 가리키고, 다른 하나는 이전 노드(후방 링크)를 가리킨다. 첫 번째 노드의 후방 링크와 마지막 노드의 전방 링크는 널 값을 가지거나 빈 리스트를 가리킨다.

• '''순환 연결 리스트(Circularly-linked list)''': 선두 노드와 꼬리 노드를 서로 연결한 리스트이다. 순환 리스트에는 단방향과 양방향이 있다. 순환 리스트를 탐색할 때는 임의의 노드에서 시작하여 원하는 방향으로 따라가며, 최초 노드로 돌아올 때까지 계속한다. 이러한 특성 때문에 순환 리스트는 데이터 저장용 버퍼 관리에 자주 사용되며, 하나의 노드를 사용하는 스레드(또는 프로세스)가 다른 모든 노드를 참조하고 싶을 때 편리하다.

3. 1. 단일 연결 리스트

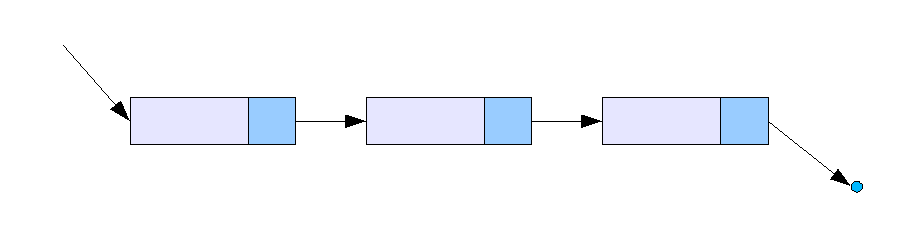
단일 연결 리스트는 각 노드에 자료 공간과 한 개의 포인터 공간이 있고, 각 노드의 포인터는 다음 노드를 가리킨다.^[2] '값' 필드와 '다음' 필드를 가진 노드로 구성되며, '다음' 필드는 다음 노드를 가리킨다. 단일 연결 리스트에서 수행할 수 있는 연산에는 삽입, 삭제 및 순회가 있다.^[2]

단일 연결 리스트는 가장 단순한 연결 리스트로, 노드마다 하나의 링크를 갖는다. 이 링크는 리스트 상의 다음 노드를 가리키며, 리스트의 마지막 노드라면 Null 값을 저장하거나 빈 리스트를 가리킨다.

노드의 데이터 구조에는 두 개의 필드가 있다. List의 "firstNode"라는 필드가 리스트의 첫 번째 노드(빈 리스트의 경우 "null")를 가리킨다고 가정한다.

'''record''' ''Node'' {

data // 노드에 저장되는 데이터

next // 다음 노드에 대한 참조 (마지막 노드의 경우 null)

}

'''record''' ''List'' {

''Node'' firstNode // 리스트의 첫 번째 노드를 가리킨다(빈 리스트의 경우 null)

}

단방향 리스트를 따라가는 것은 간단하며, 첫 번째 노드에서 각 노드의 "next" 링크를 끝까지 따라간다.

node := list.firstNode

'''while''' node ≠ null {

''(node.data 에 무언가를 한다)''

node := node.next

}

다음 코드는 단방향 리스트 상의 특정 노드 다음에 새로운 노드를 삽입한다. 특정 노드 앞에 노드를 삽입할 수는 없다. 그럴 경우에는 삽입 위치 앞의 노드를 찾아야 한다.

'''function''' insertAfter(''Node'' node, ''Node'' newNode) { // newNode를 node 다음에 삽입

newNode.next := node.next

node.next := newNode

}

리스트의 맨 앞에 노드를 추가하려면 다른 함수가 필요하다. 이 경우, firstNode를 갱신해야 한다.

'''function''' insertBeginning(''List'' list, ''Node'' newNode) { // 현재 첫 번째 노드 앞에 노드를 삽입

newNode.next := list.firstNode

list.firstNode := newNode

}

마찬가지로, 지정된 노드의 다음 노드를 삭제하는 함수와 리스트의 첫 번째 노드를 삭제하는 함수를 나타낸다. 특정 노드를 찾아 삭제하려는 경우, 그 앞의 노드를 기억해야 한다.

'''function''' removeAfter(''Node'' node) { // 이 노드의 다음 노드를 삭제

obsoleteNode := node.next

node.next := node.next.next

destroy obsoleteNode

}

'''function''' removeBeginning(''List'' list) { // 첫 번째 노드를 삭제

obsoleteNode := list.firstNode

list.firstNode := list.firstNode.next // 삭제될 노드의 다음을 가리킴

destroy obsoleteNode

}

removeBeginning()은 삭제할 노드가 마지막 노드였을 경우 "list.firstNode"를 "null"로 만든다.

역방향으로 반복할 수 없기 때문에, "insertBefore"나 "removeBefore"와 같은 연산을 효율적으로 구현할 수 없다.

두 개의 단방향 리스트를 연결하려는 경우, 리스트의 마지막 노드를 항상 가지고 있지 않으면 효율적으로 처리할 수 없다.

3. 2. 이중 연결 리스트

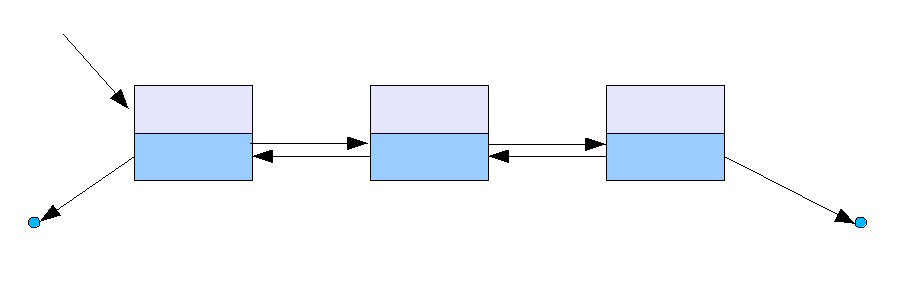
이중 연결 리스트는 단일 연결 리스트와 비슷하지만, 각 노드가 두 개의 포인터(링크)를 가진다. 각각의 포인터는 앞의 노드와 뒤의 노드를 가리킨다.

'''이중 연결 리스트'''(doubly-linked list)는 각 노드가 두 개의 링크를 가지는 연결 리스트이다. 하나는 다음 노드(전방 링크)를 가리키고, 다른 하나는 이전 노드(후방 링크)를 가리킨다. 리스트의 첫 번째 노드는 이전 노드가 없으므로 후방 링크는 널(null) 값을 저장하거나 빈 리스트를 가리킨다. 리스트의 마지막 노드는 다음 노드가 없으므로 전방 링크는 널 값을 저장하거나 빈 리스트를 가리킨다.

XOR 연결 리스트를 사용하면 이중 연결 리스트의 두 링크를 하나의 워드로 나타낼 수 있지만, 이 기법은 일반적으로 사용되지 않는다.

양방향 리스트는 업데이트해야 할 포인터가 늘어나지만, 역방향 포인터로 리스트상의 이전 요소를 참조할 수 있으므로, 조작에 필요한 정보가 줄어든다. 이로 인해 새로운 조작이 가능해지고, 특수한 경우에만 필요한 함수가 불필요해진다. 노드에는 이전 요소를 가리키는 "prev" 필드가 추가된다. 또한 리스트 구조의 "lastNode"가 마지막 노드를 가리킨다. 빈 리스트의 경우, "list.firstNode"와 "list.lastNode"는 모두 "null"이다.

3. 3. 원형 연결 리스트

원형 연결 리스트는 일반적인 연결 리스트에서 마지막 노드와 처음 노드를 연결하여 원형으로 만든 구조이다.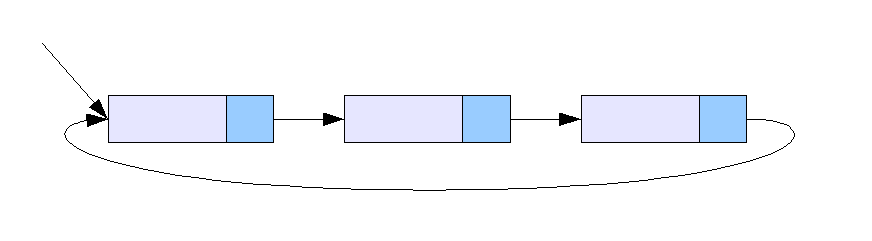

일반적인 연결 리스트에서 마지막 노드의 링크 필드는 널 참조를 포함하여 더 이상 노드가 없음을 나타낸다. 하지만 원형 연결 리스트에서는 마지막 노드가 리스트의 첫 번째 노드를 가리키도록 하여 리스트를 '순환' 또는 '원형 연결' 형태로 만든다.^[11]

원형 이중 연결 리스트의 경우에는 첫 번째 노드도 리스트의 마지막 노드를 가리킨다.

순환 연결 리스트는 선두 노드와 꼬리 노드를 서로 연결하며, 단방향과 양방향 두 가지 종류가 있다. 순환 리스트를 탐색할 때는 임의의 노드에서 시작하여 원하는 방향으로 따라가며, 최초 노드로 돌아올 때까지 계속할 수 있다. 이러한 특성 때문에 순환 리스트는 데이터 저장용 버퍼 관리에 자주 사용되며, 하나의 노드를 사용하는 스레드(또는 프로세스)가 다른 모든 노드를 참조하고 싶을 때 편리하다.

'''단방향 순환 연결 리스트'''는 각 노드가 선형 단방향 연결 리스트와 마찬가지로 하나의 링크를 가지지만, 마지막 노드는 첫 번째 노드를 가리킨다. 새로운 노드를 삽입할 때는 이미 참조를 가지고 있는 노드의 다음 위치에만 삽입할 수 있다. 따라서, 단방향 순환 연결 리스트에서는 마지막 노드를 가리키는 참조를 유지하는 경우가 많으며, 이를 통해 첫 번째 위치에 빠르게 삽입하거나 첫 번째 노드에서 마지막 노드까지 순차적으로 탐색할 수 있다.^[11]

'''양방향 원형 연결 리스트'''는 각 노드가 선형 양방향 리스트와 마찬가지로 두 개의 링크를 갖지만, 머리 노드의 뒤쪽 링크는 꼬리 노드를 가리키고, 꼬리 노드의 앞쪽 링크는 머리 노드를 가리킨다. 양방향 리스트와 마찬가지로 삽입과 삭제는 해당 위치에 인접한 노드에 대한 참조가 하나만 있으면 빠르게 수행할 수 있다.

순환 리스트는 노드가 고리 모양으로 연결되어 있기 때문에 "null"을 사용하지 않는다. 큐와 같이 전후 관계가 있는 리스트에서는 리스트의 마지막 노드에 대한 참조를 유지해야 한다. 순환 리스트에서는 마지막 노드의 다음 노드가 첫 번째 노드이다. 요소의 마지막에 추가하거나 처음에서 삭제하는 것은 상수 시간에 가능하다.

순환 리스트의 장점은 임의의 노드에서 시작하여 리스트 전체를 탐색할 수 있다는 것이다. 이 때문에 "firstNode"나 "lastNode"를 유지할 필요가 없는 경우가 많지만, 빈 리스트를 나타내기 위해서는 어떤 특별한 표현이 필요하다. 예를 들어, "lastNode"에 "null"을 저장하여 빈 리스트를 나타낼 수 있다.

3. 4. 다중 연결 리스트

이전 답변에서 언급했듯이, 주어진 원본 소스는 '다중 연결 리스트' 섹션이 아닌 '센티넬 노드'에 대한 설명입니다. 따라서 '다중 연결 리스트' 섹션에 해당 내용을 작성할 수 없습니다. 요약에 제시된 내용에 해당하는 원본 소스가 제공되지 않았으므로, 이 섹션에는 내용을 작성할 수 없습니다.

3. 5. 센티넬 노드

센티넬 노드는 모든 요소에 대해 다음 또는 이전 노드가 존재하도록 보장하고, 빈 목록조차도 최소 하나의 노드를 갖도록 함으로써 특정 목록 작업을 단순화할 수 있다.^[7] 목록 끝에 적절한 데이터 필드를 가진 센티넬 노드를 사용하여 목록 끝 검사를 제거할 수도 있다. 예를 들어, 주어진 값 ''x''를 가진 노드를 찾기 위해 목록을 스캔할 때, 센티넬의 데이터 필드를 ''x''로 설정하면 루프 내부에서 목록 끝을 테스트할 필요가 없다. 정렬된 두 개의 목록을 병합하는 경우에도 센티넬의 데이터 필드가 +∞로 설정되어 있다면, 다음 출력 노드를 선택할 때 빈 목록에 대한 특별한 처리가 필요하지 않다.^[7]

하지만 센티넬 노드는 추가 공간을 사용하며(특히 많은 짧은 목록을 사용하는 애플리케이션에서), 다른 작업(예: 새 빈 목록 생성)을 복잡하게 만들 수 있다.^[7]

원형 목록이 선형 목록을 시뮬레이션하기 위해 사용되는 경우, 마지막 데이터 노드와 첫 번째 데이터 노드 사이에 단일 센티넬 노드를 모든 목록에 추가하여 이러한 복잡성을 일부 피할 수 있다. 이 규칙에 따라, 빈 목록은 센티넬 노드 자체이며, 다음 노드 링크를 통해 자신을 가리킨다. 목록 핸들은 목록이 비어 있지 않은 경우 센티넬 앞의 마지막 데이터 노드를 가리키는 포인터여야 하고, 목록이 비어 있는 경우 센티넬 자체를 가리켜야 한다.^[7]

동일한 트릭을 사용하여 단일 센티넬 노드가 있는 원형 이중 연결 리스트로 변환하여 이중 연결된 선형 목록의 처리를 단순화할 수 있다. 그러나 이 경우 핸들은 더미 노드 자체에 대한 단일 포인터여야 한다.^[7]

선형 리스트에는 "더미 노드" 또는 "번병 노드"라고 불리는 것이 리스트의 맨 앞이나 맨 뒤에 놓이는 경우가 있다. 번병 노드에는 데이터가 저장되지 않는다. 그 목적은 모든 노드의 링크가 항상 노드의 데이터 구조를 가리키도록 보장하여 몇 가지 연산을 고속화하는 것이다. LISP에서는 그러한 설계가 되어 있으며, nil이라고 불리는 특별한 값은 단방향 리스트의 마지막을 나타내는 것으로 정해져 있다. nil은 CAR 연산에서도 CDR 연산에서도 nil을 반환하므로 일부 연산을 고속화할 수 있다. 마지막이 nil이 아닌 리스트는 부적절하다(사용할 수 없다는 것은 아니다).^[7]

번병 노드를 사용하면 모든 노드에 다음 노드나 이전 노드가 존재함을 보장할 수 있어, 특정 리스트 연산을 단순화할 수 있다. 하지만 (특히 작은 리스트를 다수 사용하는 경우) 여분의 공간을 필요로 한다는 단점이 있으며, 다른 리스트 연산은 반대로 복잡해진다. 여분의 공간 소비를 막기 위해, 번병 노드는 리스트의 첫 번째 또는 마지막 노드에 대한 참조로 재사용되기도 한다.^[7]

4. 기본 개념 및 용어

각 연결 리스트의 레코드는 '요소' 또는 '노드'라고 불린다.^[1]

각 노드에서 다음 노드의 주소를 포함하는 필드는 보통 '다음 링크' 또는 '다음 포인터'라고 불린다.^[1] 나머지 필드는 '데이터', '정보', '값', '화물', '페이로드' 등으로 알려져 있다.^[1]

리스트의 '헤드'는 첫 번째 노드이며,^[1] '테일'은 헤드 이후 나머지 리스트 또는 리스트의 마지막 노드를 가리킨다.^[1] Lisp와 일부 파생 언어에서는 다음 노드를 'cdr'이라고 부르며, 헤드 노드의 페이로드는 'car'라고 부를 수 있다.

5. 장단점

연결 리스트는 모든 상황에 완벽하게 들어맞는 자료 구조는 아니다. 어떤 경우에는 효율적이지만, 다른 경우에는 문제가 될 수 있다.

• 장점:
• 특정 위치에 노드를 삽입하거나 삭제하는 것이 매우 빠르다. (해당 위치를 이미 알고 있다면, 상수 시간 O(1) 안에 가능하다.)
• 메모리가 허용하는 한, 얼마든지 많은 요소를 추가할 수 있다. 동적 배열처럼 크기를 미리 정해둘 필요가 없다.
• 단점:
• 특정 요소를 찾기 위해서는 처음부터 순서대로 탐색해야 한다. (순차 접근, O(n) 시간 소요)
• 각 노드마다 다음 노드를 가리키는 포인터를 저장해야 하므로, 추가적인 메모리 공간이 필요하다.
• 지역성이 낮아 캐시 메모리의 효율을 제대로 활용하지 못한다.

위의 표는 배열과 비교했을 때 연결 리스트의 상대적인 장단점을 나타낸다.

연결 리스트의 종류에 따라서도 장단점이 달라진다.

• 단일 연결 리스트(singly-linked list): 가장 단순한 형태로, 각 노드는 다음 노드만을 가리킨다. 구조는 간단하지만, 한 방향으로만 탐색할 수 있다는 단점이 있다.
• 이중 연결 리스트(doubly-linked list): 각 노드가 다음 노드와 이전 노드를 모두 가리킨다. 양방향 탐색이 가능하여 더 유연하지만, 더 많은 메모리 공간을 필요로 한다.
• 원형 연결 리스트(circularly-linked list): 마지막 노드가 다시 첫 번째 노드를 가리키는 형태이다. FIFO 버퍼나 라운드 로빈 스케줄링과 같이 순환하는 구조를 표현하는 데 적합하다.

5. 1. 연결 리스트 vs. 동적 배열

• 특정 지점에서 노드에 포인터가 색인화되어 있다고 가정할 때, 리스트의 요소 삽입 또는 삭제는 상수 시간 연산이다. (그렇지 않으면 이 참조가 없으면 O(n)이다.) 반면 동적 배열에 임의의 위치에 삽입하려면 평균적으로 요소의 절반을 이동해야 하며, 최악의 경우에는 모든 요소를 이동해야 한다.
• 배열에서 슬롯을 "사용 가능"으로 표시하여 상수 시간 내에 요소를 "삭제"할 수 있지만, 이로 인해 단편화가 발생하여 반복 성능을 저해한다.
• 사용 가능한 총 메모리에 의해서만 제한되는 임의의 많은 요소를 연결 리스트에 삽입할 수 있다. 반면 동적 배열은 결국 기본 배열 자료 구조를 채우게 되며 재할당을 해야 한다.
• 재할당 비용은 삽입에 대해 평균화될 수 있으며 재할당으로 인한 삽입 비용은 여전히 상각된 O(1)이다. 이는 배열 끝에 요소를 추가하는 데 도움이 되지만, 중간 위치에 삽입하거나 제거하는 경우에도 연속성을 유지하기 위해 데이터를 이동해야 하므로 과도한 비용이 발생한다.
• 많은 요소가 제거된 배열은 너무 많은 공간을 낭비하지 않도록 크기를 조정해야 할 수도 있다.

• 단일 연결 리스트는 한 방향으로만 쉽게 이동할 수 있다. 이는 힙 정렬과 같이 인덱스로 요소를 빠르게 찾아야 하는 응용 프로그램에는 연결 리스트가 적합하지 않게 만듭니다.
• 배열 및 동적 배열에서 순차 접근은 많은 컴퓨터에서 연결 리스트보다 빠르다. 왜냐하면 최적의 참조 지역성을 가지고 있어 데이터 캐싱을 잘 활용하기 때문이다.

• 이는 문자 또는 부울 값과 같은 작은 데이터 항목의 리스트에는 실용적이지 않게 만든다. 링크에 대한 저장 오버헤드가 데이터 크기의 2배 이상일 수 있기 때문이다.
• 반면, 동적 배열은 데이터 자체에 대한 공간만 필요하다 (그리고 매우 적은 양의 제어 데이터).^[6]
• 새로운 각 요소에 대해 별도로 메모리를 할당하는 것은 느리고, 단순한 할당기를 사용하면 낭비적일 수 있다. 이러한 문제는 일반적으로 메모리 풀을 사용하여 해결된다.

• 언롤드 연결 리스트는 각 리스트 노드에 여러 요소를 저장하여 참조에 대한 메모리 오버헤드를 줄이는 동시에 캐시 성능을 향상시킨다.
• CDR 코딩도 이와 동일하게 수행하며, 참조를 실제 참조된 데이터로 대체하여 참조 레코드의 끝에서 확장한다.

• 요세푸스 문제는 한 무리의 사람들이 원을 이루어 서 있는 방식으로 작동하는 선출 방식이다.
• 미리 결정된 사람부터 시작하여 원을 따라 ''n''번 셀 수 있다. ''n''번째 사람에 도달하면 원에서 제거하고 구성원이 원을 닫아야 한다.
• 이 프로세스는 한 사람만 남을 때까지 반복된다. 그 사람이 선거에서 승리한다.
• 이는 연결 리스트와 동적 배열의 강점과 약점을 보여준다. 사람들을 원형 연결 리스트의 연결된 노드로 간주하면 연결 리스트가 노드를 얼마나 쉽게 삭제할 수 있는지 보여준다.
• 그러나 연결 리스트는 제거할 다음 사람을 찾는 데 어려움을 겪을 것이며 해당 사람을 찾을 때까지 리스트를 검색해야 한다.
• 반면 동적 배열은 노드 (또는 요소)를 삭제하는 데 어려움을 겪는다. 배열에서 하나의 노드를 제거하려면 모든 요소를 하나씩 위로 이동해야 하기 때문이다.
• 그러나 배열에서 해당 위치를 직접 참조하여 원에서 ''n''번째 사람을 찾는 것은 매우 쉽다.

• 그러나 균형을 유지하기 위해 트리 조작 오버헤드로 인해 삽입 및 삭제 작업이 더 비쌉니다.
• 트리가 자동으로 균형 상태를 유지하도록 하는 체계가 있다. AVL 트리 또는 레드-블랙 트리이다.

• 그러나, 정렬된 배열이나 트리 구조와 달리, 데이터의 검색은 ''O(n)'' 시간이 걸린다는 단점이 있다 (정렬되지 않은 배열은 선형 리스트와 같은 "O(n)"의 검색 시간이다).

연결 리스트는 배열과 비교했을 때 리스트에서는 요소의 삽입이 무제한으로 가능하다는 장점이 있다, 하지만 배열은 크기가 정해져 있어 한계가 있으며, 배열을 늘리려 해도 메모리 단편화 때문에 불가능할 수 있다. 마찬가지로, 배열에서 많은 요소를 삭제하면 공간 낭비가 발생하거나 크기를 줄여야 할 필요가 생긴다.

여러 리스트가 꼬리 부분을 공유함으로써 더 많은 메모리를 절약할 수 있는 경우도 있다.

• 즉, 머리가 여러 개 있고, 꼬리가 하나인 구조가 가능하다.
• 이를 사용하여, 어떤 데이터의 이전 버전과 새 버전을 동시에 보존할 수 있으며, 간단한 영속 데이터 구조의 예시가 된다.

• 단방향 리스트는 한 방향으로만 따라갈 수 있다. 따라서, 힙 정렬처럼 인덱스를 통해 빠르게 요소를 참조해야 하는 경우, 연결 리스트는 적합하지 않다.
• 순차 접근도 많은 머신에서는 연결 리스트보다 배열이 더 빠르다. 이는 캐시 메모리 효과와 참조 지역성에 의한 것이다. 연결 리스트는 캐시 메모리로부터 거의 아무런 이점도 얻지 못한다.

• 이 때문에 문자나 불리언형과 같은 작은 데이터 요소를 연결 리스트로 조작하는 것은 (한 문자마다 노드를 할당하여 문자열 조작을 구현하는 등), 속도 면에서도 메모리 소비 면에서도 낭비가 많아 현실적이지 않다.

• Unrolled linked list는 각 노드에 여러 요소를 저장하는 것으로, 캐시 성능을 향상시키고, 참조 시 메모리 오버헤드를 줄인다.
• CDR 코딩도 참조를 참조해야 할 실제 데이터로 대체함으로써 유사한 효과를 얻을 수 있다.

• 요세푸스 문제는, 사람들이 원을 이루어 서 있는 상황에서, 그중 한 명을 선택하는 것이다.
• 어떤 사람을 시작점으로 하여, 특정 방향으로 ''n'' 명을 세어 나간다. ''n'' 번째 사람에 도달하면, 그 사람을 원에서 제거하고, 남은 사람들로 한 바퀴 작은 원을 만든다.
• 그리고 다시 ''n'' 번째까지 세어 나간다. 이를 한 명만 남을 때까지 반복하고, 마지막에 남은 사람이 선택된 사람이 된다.
• 이것을 순환 리스트를 사용하여 나타내는 것은 직접적이고 알기 쉬우며, 노드의 삭제도 간단하다.
• 그러나, 순환 리스트에서는, 현재 노드에서 ''n'' 번째 노드를 찾으려면, 리스트를 순서대로 따라갈 수밖에 없다. 배열의 경우 인덱스 계산으로 즉시 찾을 수 있다.
• 반면, 배열에서는 요소(노드)의 삭제가 쉽지 않고, ''n'' 번째 노드를 즉시 찾는다는 장점을 살리려면, 노드를 삭제했을 때 남은 요소를 채워 넣어야 한다.

5. 2. 단일 연결 vs. 이중 연결

5. 3. 선형 연결 vs. 원형 연결

6. 응용

연결 리스트는 스택, 큐 등 다른 자료 구조를 구현하는 데 사용된다.

노드의 데이터 필드가 또 다른 연결 리스트를 가리키도록 하여 다양한 자료 구조를 리스트로 표현할 수 있다. 이는 LISP에서 유래된 방식으로, LISP에서는 연결 리스트가 주요 자료 구조였으며, 현재는 함수형 프로그래밍 언어에서 널리 사용된다.

연결 리스트를 사용하여 연관 배열을 구현하는 것을 '''연관 리스트'''라고 부르기도 한다. 그러나 이러한 방식은 균형 이진 탐색 트리와 같은 다른 자료 구조에 비해 성능이 떨어지는 경우가 많다. 다만, 트리 구조의 하위 집합을 넘어 동적으로 연결 리스트를 생성하여 데이터를 효율적으로 처리하는 데 사용될 수 있다.

7. 구현 (C 언어)

c

#include /* printf 함수를 사용하기 위해 포함 */

#include /* malloc 함수를 사용하기 위해 포함 */

typedef struct ns {

int data;

struct ns *next;

} node;

node *list_add(node **p, int i) { /* 머리(head)에 노드 추가 */

node *n = malloc(sizeof(node));

n->next = *p;

• p = n;

• p = (*p)->next;

8. 관련 자료 구조

• 스택과 큐는 종종 연결 리스트를 사용하여 구현되며, 허용되는 연산 유형을 제한한다.^[1]
• 스킵 리스트는 여러 계층의 포인터로 보강된 연결 리스트로, 많은 수의 요소를 빠르게 건너뛸 수 있다. 최하위 계층까지 이 과정이 계속된다.^[1]
• 이진 트리는 요소 자체가 동일한 성격의 연결 리스트인 연결 리스트의 한 유형으로 볼 수 있다. 각 노드는 하나 또는 두 개의 다른 연결 리스트(하위 트리)의 첫 번째 노드를 참조한다.^[1]
• 언롤드 연결 리스트는 각 노드에 데이터 값의 배열이 포함된 연결 리스트이다. 캐시 성능을 향상시키고 메모리 오버헤드를 줄인다.^[1]
• 해시 테이블은 연결 리스트를 사용하여 해시 테이블의 동일한 위치에 해시되는 항목의 체인을 저장할 수 있다.^[1]
• 힙은 연결 리스트의 정렬 속성 일부를 공유하지만, 주로 배열을 사용하여 구현된다. 노드 간 참조 대신 현재 데이터 인덱스를 사용하여 다음 및 이전 데이터 인덱스를 계산한다.^[1]
• 자기 구성 리스트는 데이터 검색 시간을 줄이기 위해 일반적으로 액세스되는 노드를 리스트의 헤드에 유지하는 휴리스틱을 기반으로 노드를 재정렬한다.^[1]

참조

_[1] 서적 The Art of Computer Programming Addison-Wesley
_[2] 웹사이트 The NT Insider:Kernel-Mode Basics: Windows Linked Lists http://www.osronline[...] 2015-07-31
_[3] 웹사이트 VICE – Catch the hookers! (Plus new rootkit techniques) https://www.cs.dartm[...] 2021-08-31
_[4] 간행물 Resizable Arrays in Optimal Time and Space (Technical Report CS-99-09) http://www.cs.uwater[...] Department of Computer Science, University of Waterloo
_[5] 논문 Purely Functional Random-Access Lists
_[6] 문서
_[7] 서적 Data Structures with C++ using STL Prentice-Hall 2002
_[8] 서적 Purely Functional Random-Access Lists http://cs.oberlin.ed[...] ACM Press 2015-05-07
_[9] 웹사이트 RECURSIVE FUNCTIONS OF SYMBOLIC EXPRESSIONS AND THEIR COMPUTATION BY MACHINE (Part I) (12-May-1998) https://www-formal.s[...] 2024-04-07
_[10] 웹사이트 McCarthy et al. LISP I Programmer's Manual. — Software Preservation Group https://www.software[...] 2024-04-07
_[11] 간행물 Data Structures and Algorithms with Object-Oriented Design Patterns in Java http://www.brpreiss.[...] Wiley 1999
_[12] 문서